It is the Stanley Cup finals for North American math students – a competition so prestigious that a successful score is virtually a ticket to postgraduate studies at an elite university. The University of Toronto has an illustrious track record at the William Lowell Putnam Mathematical Competition, a contest that dates back to 1938. U of T teams always make it into the top 10, and have finished in the top five 31 times, including four firsts – the inaugural competition among them.
Two former U of T students – Ravi Vakil (BSc 1992 TRIN, MSc 1992), now a Stanford professor, and J.P. Grossman (BSc 1996 TRIN), who works for D.E. Shaw Research in New York – have earned the distinction of Putnam Fellow for placing among the top five individuals in a given year. The honours come with a $2,500 prize. U of T’s Victoria Krakovna took the $1,000 Elizabeth Lowell Putnam Prize for top female participant in 2008.
While about 50 U of T students planned to write the test in early December (there were more than 4,000 competitors in total, from across Canada and the U.S.), U of T math prof Ilia Binder also selects a three-person team to represent the university. This year’s team will be led by fourth-year math student Alexander Remorov, who was born in Moscow and moved to Canada when he was 12. (The other two members are Keith Ng and Jonathan Zung.) Remorov has written the Putnam competition three times, ranking 27th overall last year. He credits his problem-solving ability to the rigorous training provided in Russian middle schools. “They push you a lot.”
But Putnam veterans also know that strategic savvy helps when it comes to placing well in the competition. Spread out over two three-hour sessions, the test consists of 12 problems, each of which is scored out of 10. But according to Putnam tradition, the markers will assign scores either in the 8 to 10 range, or from 0 to 2. In other words, you don’t get much in the way of part marks for a good try.
Remorov says the answer to some problems is almost immediately apparent (to him, at least), and can be written up in an elegant proof in just a few minutes. Others, however, can consume an hour of hard thinking. “Six hours seems like a long time but it is actually more of a speed competition,” he muses. In fact, some participants have been known to be selective about what they answer, aiming to maximize their score by getting full marks on a handful of problems rather than minimal marks on several.
Last year, Remorov took a run at 10 and ended up solving a highly respectable eight. “It’s very hard to solve all 12,” he adds, noting that fewer than 10 participants in the 73-year history of the competition have achieved a perfect score.
Sample questions from previous Putnam Competitions:
1. Four points are chosen uniformly and independently at random in the interior of a given circle. Find the probability that they are the vertices of a convex quadrilateral.
2. There are 2010 boxes labeled B1, B2, …, B2010, and 2010n balls have been distributed among them, for some positive integer n. You may redistribute the balls by a sequence of moves, each of which consists of choosing an i and moving exactly i balls from box Bi into any one other box. For which values of n is it possible to reach the distribution with exactly n balls in each box, regardless of the initial distribution of balls?
3. Find all pairs of polynomials p(x) and q(x) with real coefficients for which p(x)q(x + 1) − p(x + 1)q(x) = 1.
Recent Posts
People Worry That AI Will Replace Workers. But It Could Make Some More Productive
These scholars say artificial intelligence could help reduce income inequality
A Sentinel for Global Health
AI is promising a better – and faster – way to monitor the world for emerging medical threats
The Age of Deception
AI is generating a disinformation arms race. The window to stop it may be closing


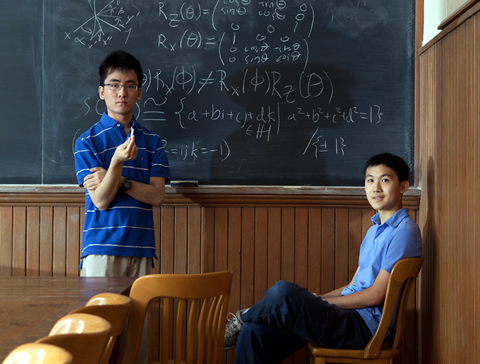


4 Responses to “ Proof of Genius ”
Good luck team! Also, thank you for a very nicely written article and choice of sample problems.
How is it that, according to the article, Ravi Vakil got *both* BSc and MSc in the *same year*, 1992?
Mr. Vakil is a very clever fellow!
My cousin Harold Seigel, who died this year, earned a PhD in geophysics. He was a Putnam champion along with D.A.S. Fraser PhD (statistics) and Perham Stanley PhD (mathematics and an actuary). There is a picture of the early U of T Putnam history in Martin Friedland's history of U of T. Many of those listed became actuaries.